Про закон Ома в популярном изложении
Электрический ток и опасное напряжение невозможно услышать (за исключением гудящих высоковольтных линий и электроустановок). Токоведущие части, находящиеся под напряжением, ничем не отличаются по внешнему виду.
Невозможно узнать их и по запаху, и повышенной температурой в штатных режимах работы они не отличаются. Но включаем в безмолвную и тихую розетку пылесос, щелкаем выключателем – и энергия словно берется из ниоткуда, сама по себе, материализуясь в виде шума и компрессии внутри бытового прибора.
Опять же, если мы воткнем в разъемы розетки два гвоздя и возьмемся за них, то буквально всем своим телом ощутим реальность и объективность существования электрического тока. Делать это, конечно, настоятельно не рекомендуется.
Но примеры с пылесосом и гвоздями наглядно демонстрируют нам, что изучение и понимание основных законов электротехники способствует безопасности при обращении с бытовым электричеством, а также устранению суеверных предубеждений, связанных с электрическим током и напряжением.
Итак, рассмотрим один, самый ценный закон электротехники, который полезно знать. И попытаемся сделать это в как можно более популярной форме.
Открытие закона Ома
В 1827 г. немецкий физик Георг Симон Ом сформулировал закон, связывающий величины электрического тока, электродвижущей силы батареи и сопротивления простой электрической цепи, составленной из батареи и соединяющих ее полюса последовательно включенных разнородных проводников. Кроме того, он обнаружил, что различные вещества оказывают электрическому току различное сопротивление.

Ом экспериментально установил, что в последовательной цепи, составленной из нескольких участков с проводниками разного сопротивления, ток во всех участках одинаков, различна только разность потенциалов на проводниках, которую Ом назвал «падением напряжения».
В нормальном, несверхпроводящем металлическом проводнике имеет место закон Ома. Для участка проводника, не содержащего источника электродвижущей силы (гальванического элемента, аккумулятора, генератора, термопары, источника фотоэдс и т. д.), закон Ома заключается в том, что сила тока пропорциональна разности потенциалов на концах участка. Коэффициент пропорциональности называют сопротивлением.
Первая запись о законе Ома в лабораторной книге Георга Симона Ома сегодня хранится в архивах Немецкого музея в Мюнхене:

Открытие закона Ома было очень важным этапом исследований электрических и магнитных явлений, имевших большое практическое значение. Закон Ома и открытые в дальнейшем законы Кирхгофа впервые дали возможность производить расчеты электрических цепей и легли в основу зародившейся электротехники.
Виды законов Ома
1. Дифференциальная форма записи закона Ома
Самый главный закон электротехники – это, конечно, закон Ома. О его существовании знают даже люди, не имеющие отношения к электротехнике. Но между тем вопрос «А знаешь ли ты закон Ома?» в технических ВУЗах является ловушкой для зарвавшихся и самонадеянных школяров. Товарищ, разумеется, отвечает, что закон Ома знает отлично, и тогда к нему обращаются с просьбой привести этот закон в дифференциальной форме. Тут-то и выясняется, что школяру или первокурснику еще учиться и учиться.
Однако дифференциальная форма записи закона Ома на практике почти неприменима. Она отражает зависимость между плотностью тока и напряженностью поля:
где G – это проводимость цепи; Е – напряженность электрического тока.
Все это – попытки выразить электрический ток, принимая во внимание только физические свойства материала проводника, без учета его геометрических параметров (длина, диаметр и тому подобное). Дифференциальная форма записи закона Ома – это чистая теория, знание ее в быту совершенно не требуется.
2. Интегральная форма записи закона Ома для участка цепи
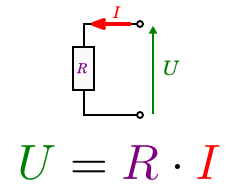
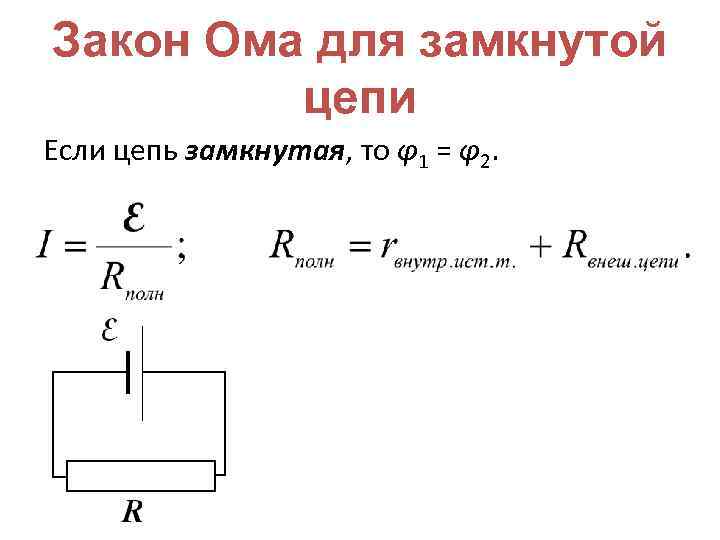
Иное дело – интегральная форма записи. Она тоже имеет несколько разновидностей. Самой популярной из них является закон Ома для участка цепи: I=U/R
Говоря по-другому, ток в участке цепи всегда тем выше, чем больше приложенное к этому участку напряжение и чем меньше сопротивление этого участка.
Вот этот «вид» закона Ома просто обязателен к запоминанию для всех, кому хоть иногда приходится иметь дело с электричеством. Благо, и зависимость-то совсем простая. Ведь напряжение в сети можно считать неизменным.
Для розетки оно равно 220 вольт. Поэтому получается, что ток в цепи зависит только от сопротивления цепи, подключаемой к розетке. Отсюда простая мораль: за этим сопротивлением надо следить.
Короткие замыкания, которые у всех на слуху, случаются именно по причине низкого сопротивления внешней цепи. Предположим, что из-за неправильного соединения проводов в ответвительной коробке фазный и нулевой провода оказались напрямую соединены между собой. Тогда сопротивление участка цепи резко снизится практически до нуля, а ток так же резко возрастет до очень большой величины.
Если электропроводка выполнена правильно, то сработает автоматический выключатель, а если его нет, или он неисправен или подобран неправильно, то провод не справится с возросшим током, нагреется, расплавится и, возможно, вызовет пожар.
Но бывает, что приборы, включенные в розетку и отработавшие уже далеко не один час, становятся причиной короткого замыкания. Типичный случай – вентилятор, обмотки двигателя которого подверглись перегреву из-за заклинивания лопастей.
Изоляция обмоток двигателя не рассчитана на серьезный нагрев, она быстро приходит в негодность. В результате появляются межвитковые короткие замыкания, которые снижают сопротивление и, в соответствии с законом Ома, также ведут к увеличению тока.
Повышенный ток, в свою очередь, приводит изоляцию обмоток в полную негодность, и наступает уже не межвитковое, а самое настоящее, полноценное короткое замыкание. Ток идет помимо обмоток, сразу из фазного в нулевой провод. Правда, все сказанное может случиться только с совсем простым и дешевым вентилятором, не оборудованным тепловой защитой.

Шпаргалка по закону Ома для участка цепи:
Закон Ома для переменного тока
Надо отметить, что приведенная запись закона Ома описывает участок цепи с постоянным напряжением. В сетях переменного напряжения существует дополнительное реактивное сопротивление, а полное сопротивление приобретает значение квадратного корня из суммы квадратов активного и реактивного сопротивления.
Закон Ома для участка цепи переменного тока принимает вид: I=U/Z,
где Z – полное сопротивление цепи.
Но большое реактивное сопротивление свойственно, прежде всего, мощным электрическим машинам и силовой преобразовательной технике. Внутреннее электрическое сопротивление бытовых приборов и светильников практически полностью является активным. Поэтому в быту для расчетов можно пользоваться самой простой формой записи закона Ома: I=U/R.
3. Интегральная форма записи для полной цепи
Раз есть форма записи закона для участка цепи, то существует и закон Ома для полной цепи: I=E/(r+R).
Здесь r – внутреннее сопротивление источника ЭДС сети, а R – полное сопротивление самой цепи.
За физической моделью для иллюстрации этого подвида закона Ома далеко ходить не надо – это бортовая электрическая сеть автомобиля, аккумулятор в которой является источником ЭДС.
Нельзя считать, что сопротивление аккумулятора равно абсолютному нулю, поэтому даже при прямом замыкании между его клеммами (отсутствии сопротивления R) ток вырастет не до бесконечности, а просто до высокого значения.
Однако этого высокого значения, конечно, хватит для того, чтобы вызвать расплавление проводов и возгорание обшивки авто. Поэтому электрические цепи автомобилей защищают от короткого замыкания при помощи предохранителей.
Такой защиты может оказаться недостаточно, если замыкание произойдет до блока предохранителей относительно аккумулятора, или если вовсе один из предохранителей заменен на кусок медной проволоки. Тогда спасение только в одном – необходимо как можно быстрее разорвать цепь полностью, откинув «массу», то есть минусовую клемму.
4. Интегральная форма записи закона Ома для участка цепи, содержащего источник ЭДС
Следует упомянуть и о том, что есть и еще одна разновидность закона Ома – для участка цепи, содержащего источник ЭДС:
Здесь U – это разность потенциалов в начале и в окончании рассматриваемого участка цепи. Знак перед величиной ЭДС зависит от направленности ее относительно напряжения.
Воспользоваться законом Ома для участка цепи нередко приходится при определении параметров цепи, когда часть схемы недоступна для детального изучения и не интересует нас.
Допустим, она скрыта неразъемными деталями корпуса. В оставшейся схеме имеется источник ЭДС и элементы с известным сопротивлением. Тогда, замерив напряжение на входе неизвестной части схемы, можно вычислить ток, а после этого – и сопротивление неизвестного элемента.
В каких случаях не выполняется закон Ома
Закон Ома не является универсальной связью между током и напряжением. Для металлов (в несверхпроводящем состоянии) закон Ома имеет место вплоть до весьма больших плотностей тока. Для полупроводников и газов пропорциональность между током и напряжением наблюдается лишь при малых напряжениях.
Термоэлектронный ток в вакууме не подчиняется закону Ома даже при малых напряжениях — в этом случае сила тока пропорциональна U 3/2 . В вольтовой дуге с увеличением тока напряжение падает (падающая вольтамперная характеристика), так что не может быть и речи о выполнении закона Ома.
Выражение I=U/R , однако, записывают даже в случае, когда закон Ома не выполняется. Тогда оно служит определением сопротивления R = U/I . Если сопротивление не зависит от величины тока, закон Ома имеет место. Если сопротивление само меняется с изменением тока (как, например, сопротивление газа при газовом разряде), то никакой пропорциональности между напряжением и током нет, а значит, нет и закона Ома.
Выводы
Таким образом, мы можем увидеть, что «простой» закон Ома далеко не так прост, как кому-то, возможно, казалось. Зная все формы интегральной записи законов Ома, можно понять и легко запомнить многие требования электробезопасности, а также приобрести уверенность в обращении с электричеством.
Источник
Закон Ома в интегральной форме
Для того, чтобы перейти к интегральной форме записи закона Ома для участка проводника, на котором действуют две силы, введем понятие линии тока.
Линия тока – кривая, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. В этом случае вектор плотности находится из соотношения:
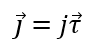
где τ ⃗ – единичный вектор касательной к линии тока.
Предположим, что удельное сопротивление (r) и напряженность поля движущих сил (E ⃗) на поперечном сечении проводника однородны, т.к. E ⃗ однородна, то j ⃗ так же однородная величина. Возьмем произвольное значение поперечного сечения цепи – S. Тогда:
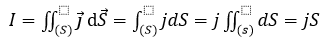
, а значит 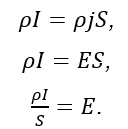
Последнее равенство до множим на dl (элементарное перемещение вдоль вектора плотности тока):
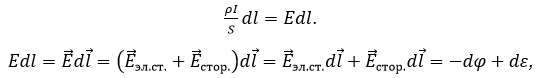
где
- dφ – элементарный сброс потенциала электростатического поля,
- dε – элементарная работа сторонних сил по перемещению единичного положительного заряда (ЭДС).
Отсюда: 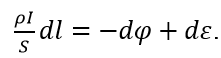
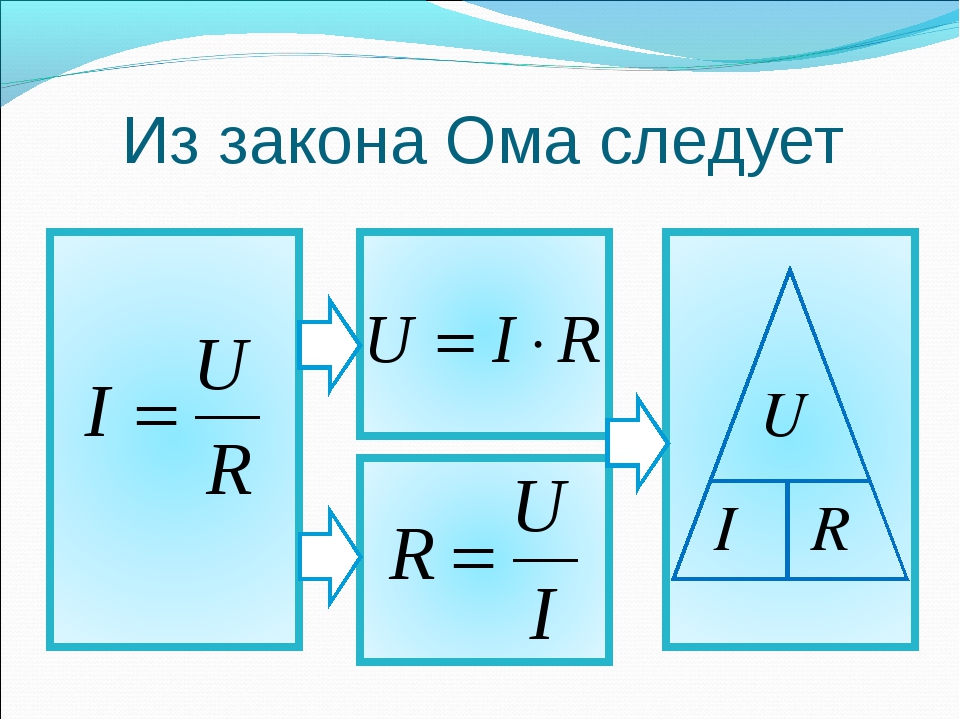
Учитывая, что ρ/S dl=dR (элементарное сопротивление), запишем закон Ома в интегральной форме:
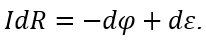
Закон Ома в интегральной форме для неоднородного участка цепи
Проинтегрируем получившееся соотношение на конкретном участке цепи постоянного тока между поперечными сечениями S1 и S2:
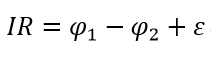
интегральный закон Ома для участка цепи
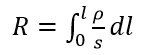
– сопротивление участка,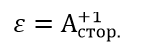
– работа сторонних сил на перемещении единичного положительного заряда по данному участку цепи ЭДС участка,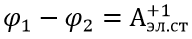
– работа электростатических сил на перемещении единичного положительного заряда по данному участку цепи (напряжение участка),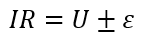
– абсолютная величина работы сил сопротивления на перемещении единичного положительного заряда по данному участку цепи (падение напряжения участка).
Запишем значение напряжения при постоянном токе:
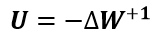
Отсюда запишем закон Ома:
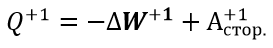
Таким образом закон Ома в интегральной форме – это закон изменения механической энергии единичного положительного заряда на этом участке. В арифметическом виде этот закон можно записать так:
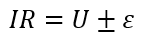
Решение задач
Какой будет плотность тока в металлическом проводнике с удельным сопротивлением ρ постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?
Пространство между пластинами плоского конденсатора заполняет неоднородное плохо проводящее вещество, удельная проводимость которого изменяется в соответствии с линейным законом: 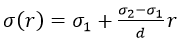
в направлении перпендикулярном пластинам. Известно, что расстояние между пластинами – d, площадь пластин конденсатора – S. Каким будет ток через этот конденсатор, если напряжение на нем станет равно U?
Формула закона Ома
Первый Закон Ома устанавливает, что разница потенциалов между двумя точками резистора пропорциональна току. Более того, согласно этому закону, соотношение между потенциалом и током всегда является постоянным для омических резисторов.
V — напряжение/электропотенциал (В);
R — электросопротивление (ом);
I — электрический ток.
В нем U является скалярной величиной и меряется в (В). Разница в электропотенциалах между двумя точками цепи, указывает на наличие электросопротивления. Когда I проходит через резистивный элемент R, происходит падение электрического потенциала. Это различие возникает из-за рассеивания энергии, называемым эффектом Джоуля. I измеряет поток зарядов через тело в (А) и прямо пропорционален сопротивлению провода.
Второй закон Ома говорит о том, что электросопротивление R представляет собой свойство из тела, которое регулирует проходимость I. Это свойство зависит от геометрических факторов тела, таких как длина или площадь сечения участка и от вызываемой величины R. Его количество зависит исключительно от материала участка.
R — электросопротивление (Ом);
ρ — удельное электросопротивление провода (Ом.м);
L — протяженность проводника (м);
S — площадь сечения провода (м2).
Омическим резистором называется любое тело, способное представлять постоянное сопротивление для данного диапазона напряжений. График напряжения как функция тока для омических резисторов является линейным. Резистор можно считать омическим в диапазоне, в котором его потенциал линейно возрастает с ростом I.
Сопротивление можно понимать как наклон линии, заданный тангенсом угла. Как известно, тангенс определяется, как отношение между противоположным и соседним сторонами, и, в случае, когда сопротивления омические, может быть рассчитан по формуле: R = U / I.
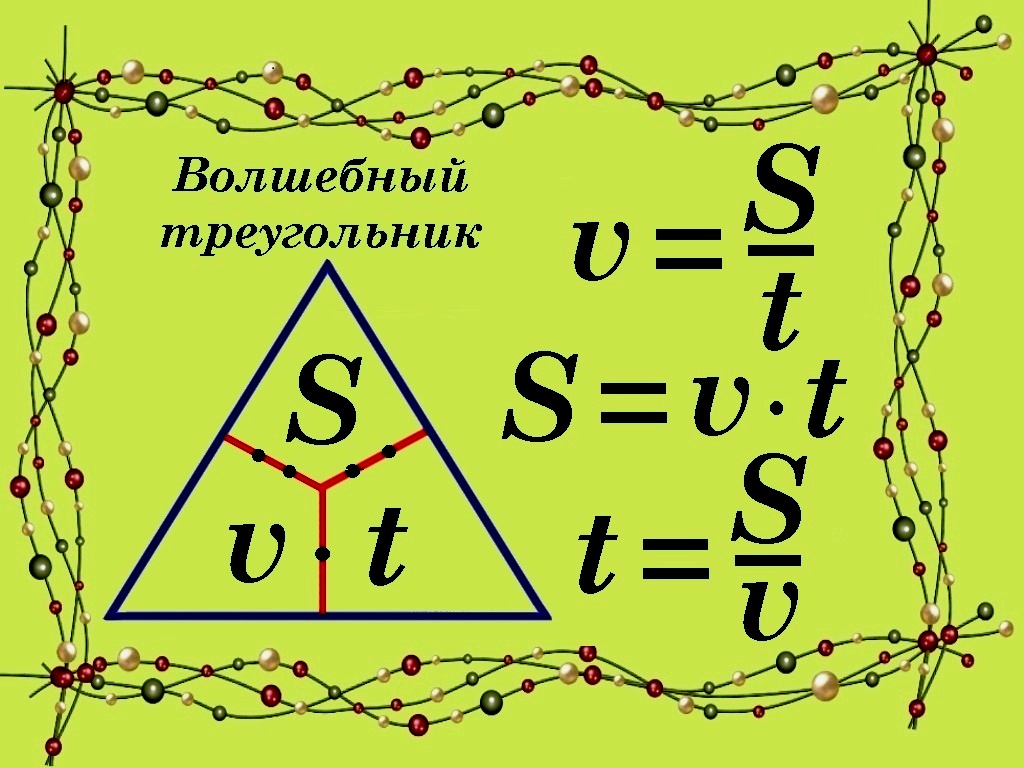
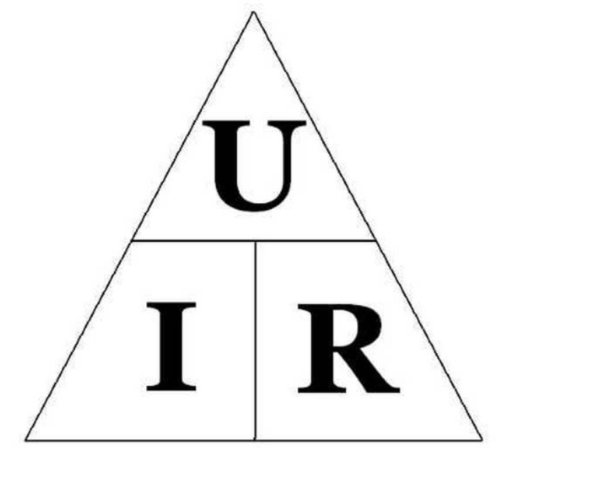
Треугольник
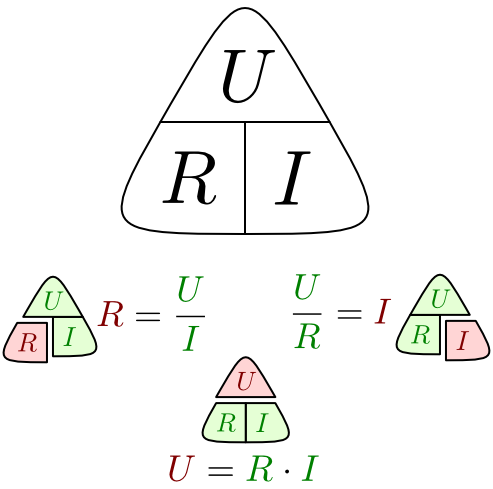
Чтобы помочь запомнить формулу, можно использовать треугольник с одной горизонтальной стороной и вершиной вверху, как пирамиду. Это иногда называют законом треугольника Ома. В верхнем его углу находится буква V, в левом углу — буква I, а в правом нижнем углу — R.
Обратите внимание! Чтобы использовать треугольник, прикрыть неизвестный параметр, а затем, рассчитать его из двух других. Если они находятся на одной линии, они умножаются, но если одна находится над другой, их следует разделить. Другими словами, если необходимо рассчитать I, напряжение делится на сопротивление, то есть V / R.
Для полной замкнутой цепи
Закон Ома для полной цепи определение — ЭДС электрического элемента аккумулятора или источника — это общая работа, выполненная внутри и снаружи элемента для переноса электрических зарядов в электроцепи. Если обозначим ЭДС аккумулятора через E (B), суммарная сила тока для полной цепи I (А), внешнее сопротивление R (Ом) и внутреннее сопротивление ячейки r по (Ом).
Тогда: E = I*R + I*r
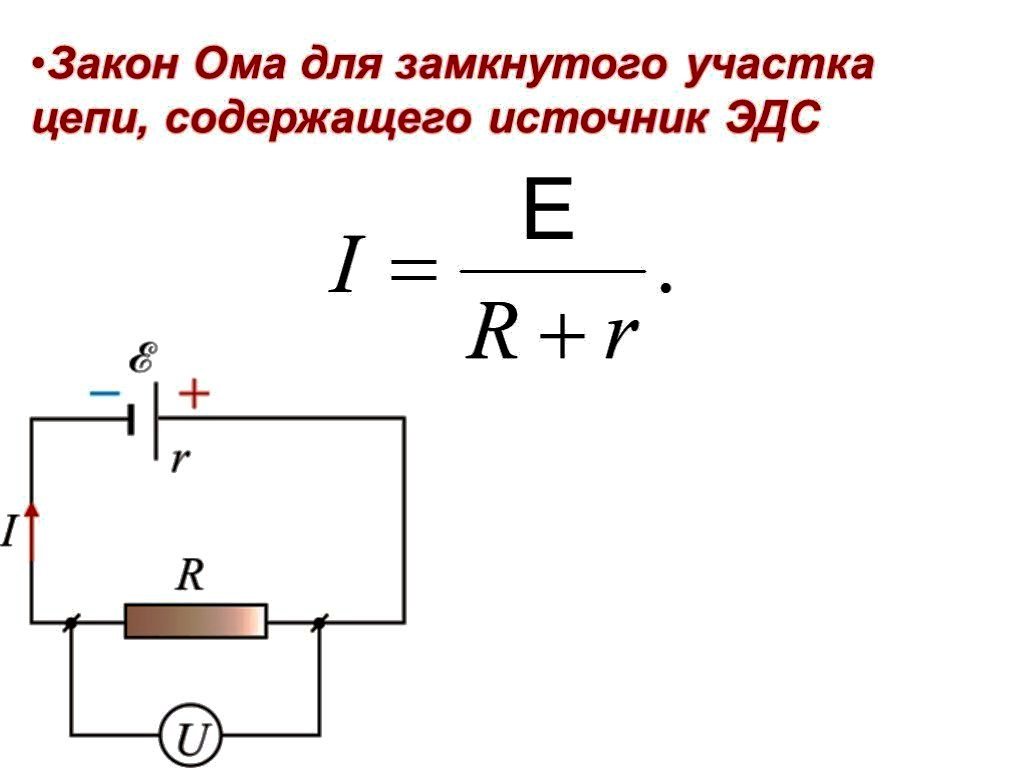
Замкнутая сеть
Это выражение известно, как закон Ома для замкнутого контура, где: I — интенсивность тока равна E общей электродвижущей силе деленной на (R + r) — общее сопротивление цепи.
Связь между ЭДС (E) электрической ячейки и напряжением на ее полюсах (V). На основании закона Ома для замкнутых цепей:
E = IR + I r, V = IR
ЭДС электрической ячейки больше, чем разность потенциалов между клеммами ее внешней цепи, когда цепь включена. Потому что внутреннее сопротивление ячейки потребляет работу для передачи I внутрь нее на основе соотношения E = V + I r и, следовательно, V Для участка цепи
Законы Ома для участка цепи применяются также часто, как и для замкнутого контура. Разница в том, что при расчете учитывается не ЭДС, а только разность потенциалов. Такой участок называется однородным. В этом случае существует особый случай, который позволяет рассчитать характеристики электрической цепи на каждом из ее элементов.
V — разность напряжений или потенциалов. Измеряется вольтметром при параллельном подключении щупов к клеммам любого элемента (сопротивления). Результирующее значение V всегда меньше, чем ЭДС.
Для переменного тока
Общим термином для сопротивления переменного I является полное сопротивление и обозначается символом Z. Треугольник используется точно также, как закон Ома в DC, за исключением того, что теперь используют сопротивление Z. Следует отметить, что при измерении переменного напряжения или тока измеритель будет показывать только правильные значения в ограниченном диапазоне частот. Обычно это справедливо для постоянного I до 400 Гц.
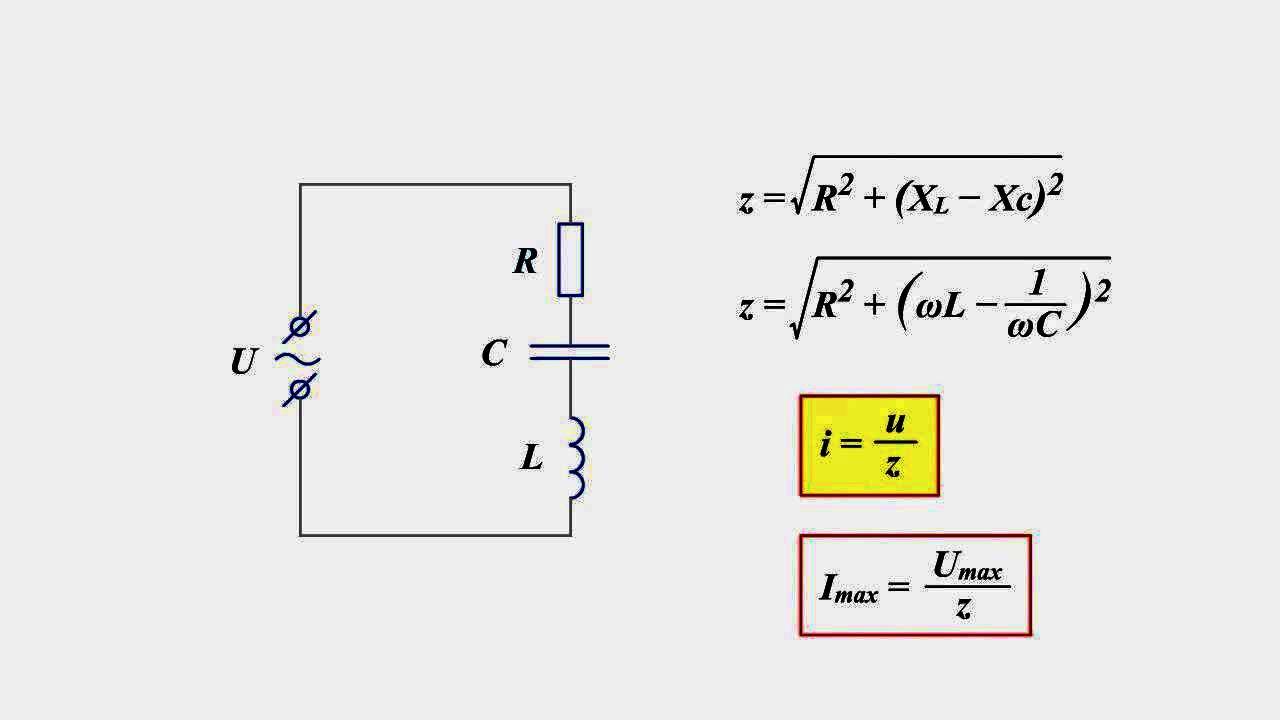
Переменный ток
Для цепей переменного тока, в которых напряжение и I находятся в фазе, может использоваться круговая диаграмма. В случае цепей переменного тока напряжение связано с I с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R для чисто резистивных цепей, где (Z = R).
V = IZ и V = IR (для чисто резистивных цепей)
Где Z = √ [R 2 + X 2]
Импеданс Z — это полное сопротивление цепей к переменному току. Он состоит из реальной части (сопротивления) и мнимой части (реактивности).
В интегральной форме
Наиболее часто в электротехнике используют омическое соотношение в интегральной форме. Если рассмотреть часть проводника, приняв для простоты, что он имеет цилиндрическую форму, с площадью поперечного сечения S, к концам которого приложена разность потенциалов Δ φ = φ 1- φ 2, то внутри проводника будет действовать электрополе с плотностью тока j = σ*Е в соответствии с Законом Ома. Если предположить, что I будет равномерен по площади сечения провода, тогда:

Интегральная форма
Если поле Е в проводнике однородно, вектор Е будет направляться вдоль оси Ох, в этом случае напряжённость поля будет взаимосвязана с потенциалом формулой
I = σ*S*dφ/dx, поэтому
Интегрируя данное выражение для всего участка провода, получится:
I* ∫ dx/dφ = φ1 — φ2
Выражение, стоящее в левой части является сопротивлением проводника R, таким образом интегральная форма Закона Ома:
I *R = φ1, φ2 = V , где:
Для проводника с формой цилиндра, где S постоянная величина R = L/(σ *S) = ρ* L/S,
где L — длина проводника, а ρ = 1/σ — удельное сопротивление.
Неоднородного участка цепи
Однако существуют компоненты электрических цепей, которые не подчиняются закону Ома, то есть их взаимосвязь между током и напряжением является нелинейной или неомической. Например, pn-переходный диод. В нем I не увеличивается линейно с приложенным напряжением для диода. Можно определить значение тока (I) для данного значения приложенного напряжения (V) по кривой, но не по закону Ома, поскольку значение «сопротивления» не является постоянной величиной.
Кроме того, I значительно увеличивается, только если приложенное напряжение положительное, а не отрицательное. Соотношение V/I для некоторой точки вдоль нелинейной кривой иногда называют статическим, хордовым или постоянным сопротивлением. Значение общего V над общим I изменяется в зависимости от конкретной точки вдоль нелинейной кривой.
Это означает, что «сопротивление постоянному току» V/I в некоторой точке кривой не совпадает с тем, которое было бы определено путем подачи переменного сигнала, имеющего пиковую амплитуду V вольт или I ампер с центром в той же точке вдоль кривой. Однако в некоторых применениях с диодами сигнал переменного тока, подаваемый на устройство, мал, и можно анализировать схему с точки зрения динамики, мало сигнальное, или инкрементное сопротивления, определяемое как сопротивление наклона кривой V-I при среднем значении напряжения. Для достаточно малых сигналов динамическое сопротивление позволяет рассчитать закон малого сопротивления Ома как приблизительно одно по наклону линии, проведенной по касательной к кривой в рабочей точке постоянного тока.
Закон Ома для участка сети однородного характера был изложен выше. Закон на нелинейном участке будет иметь следующий вид:
I = U/ R = φ1 — φ2 + E/ R, где:
φ1 — φ2 — разница потенциалов на конечных точках рассматриваемого участка сети,
R — общее сопротивление нелинейного участка цепи.
Сила тока по закону Ома
Альтернативные утверждения закона Ома заключаются в том, что I в проводнике равен разности потенциалов V на проводнике, деленной на сопротивление проводника, или просто I = V / R, и что разность потенциалов на проводнике равна произведению тока в проводнике и его сопротивления, V = IR.
В цепи, в которой разность потенциалов или напряжение постоянны, I может быть уменьшен, путем добавления большего сопротивления или увеличен путем удаления некоторого сопротивления. Закон Ома также может быть выражен в терминах электродвижущая сила, или напряжение, E — источника электрической энергии, такой как батарея, например, I = Е / R.
С изменениями закон Ома также применяется к цепям переменного тока, в которых соотношение между напряжением и током более сложное, чем для постоянных I. Именно потому, что I меняется, возникают другие формы замыкания тока, называемые реактивным сопротивлением. Сочетание сопротивления и реактивного сопротивления называется импеданс, Z. Когда импеданс, эквивалентный отношению напряжения к току, в цепи переменного тока является постоянным, обычное явление, применим закон Ома, например, V/I = Z.
Читайте также: Диффузионный ток при обратном включении
Закон Ома используется во всех отраслях электротехники для расчета значения резисторов, требуемых в цепях, и также может использоваться для определения тока, протекающего в цепи, где напряжение можно легко измерить через известный резистор. Таким образом, он применяется в огромном количестве вычислений во всех формах электрических и электронных схем — фактически везде, где течет ток.
Закон Ома для участка цепи простым языком
Вся прикладная электротехника базируется на одном догмате — это закон Ома для участка цепи. Без понимания принципа этого закона невозможно приступать к практике, поскольку это приводит к многочисленным ошибкам. Имеет смысл освежить эти знания, в статье мы напомним трактовку закона, составленного Омом, для однородного и неоднородного участка и полной цепи.
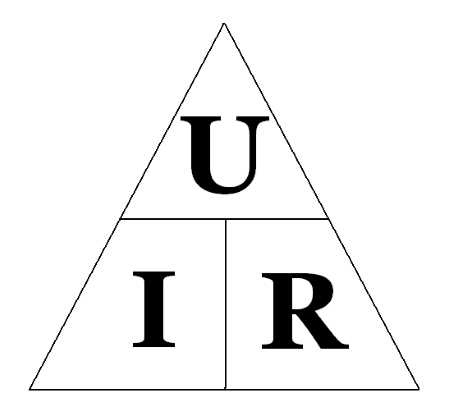
Диаграмма, упрощающая запоминание
Классическая формулировка
Этот простой вариант трактовки, известный нам со школы.
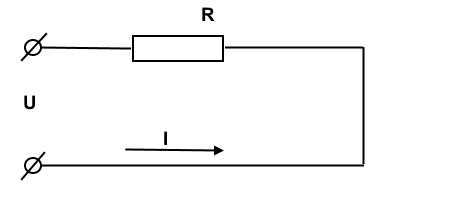
Однородный открытый участок электроцепи
Формула в интегральной форме будет иметь следующий вид:
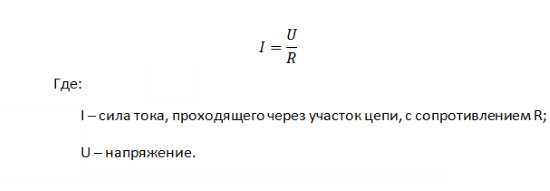
Формула в интегральной форме
То есть, поднимая напряжение, мы тем самым увеличиваем ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I». Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.
В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.
Принятые единицы измерения
Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:
- напряжение – в вольтах;
- ток в амперах
- сопротивление в омах.
Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
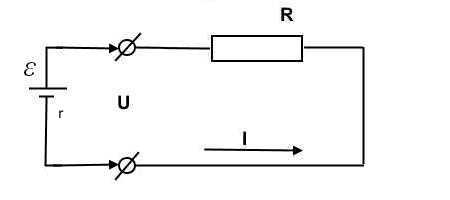
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:

Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:
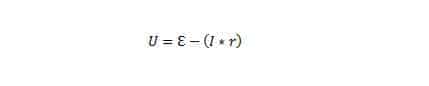
Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
Неоднородный участок цепи постоянного тока
Под таким типом подразумевается участок, где помимо электрического заряда производится воздействие других сил. Изображение такого участка показано на рисунке ниже.
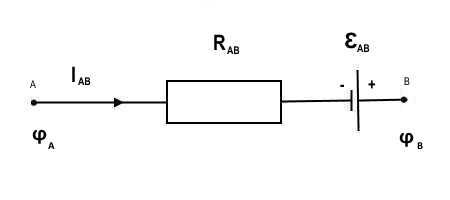
Схема неоднородного участка
Формула для такого участка (обобщенный закон) будет иметь следующий вид:

Формула для неоднородного участка цепи
Переменный ток
Если в схема, подключенная к переменному току снабжена емкостью и/или индуктивностью (катушкой), расчет производится с учетом величин их реактивных сопротивлений. Упрощенный вид закона будет выглядеть следующим образом:
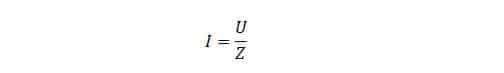
Где «Z» представляет собой импеданс, это комплексная величина, состоящая из активного (R) и пассивного (Х) сопротивлений.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
Интересно по теме: Как проверить стабилитрон.
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
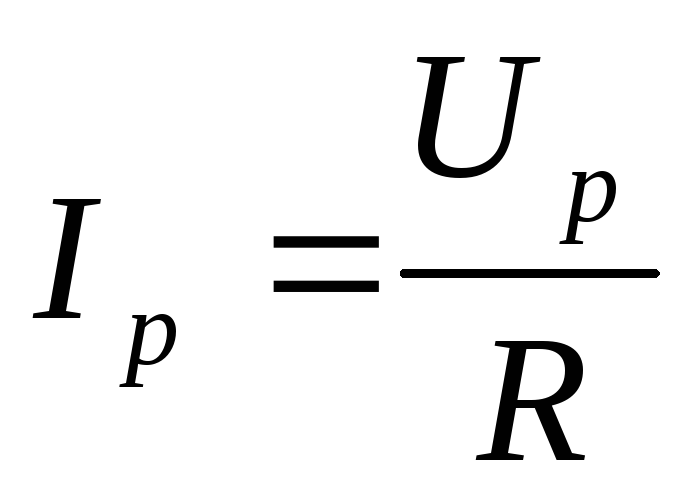
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
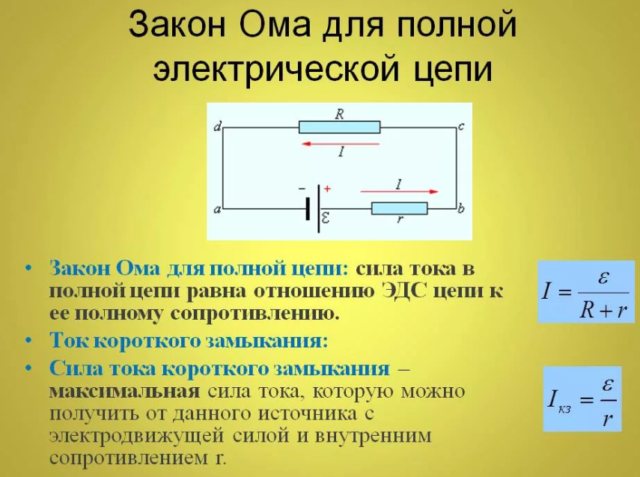
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Следствия закона Ома.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
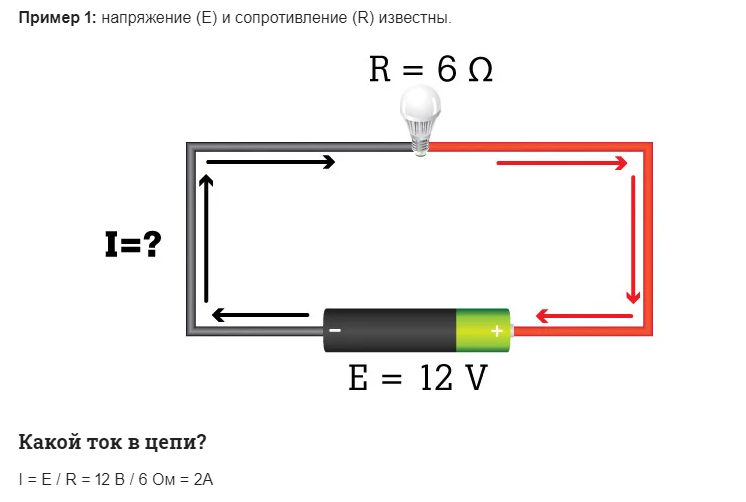
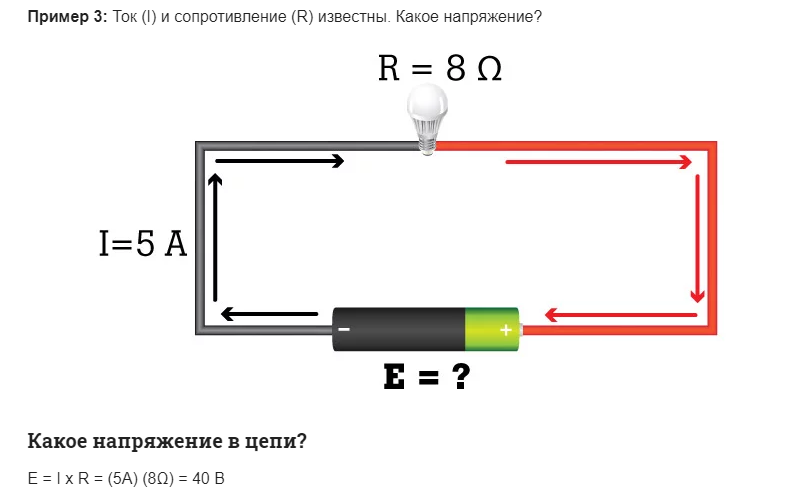
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
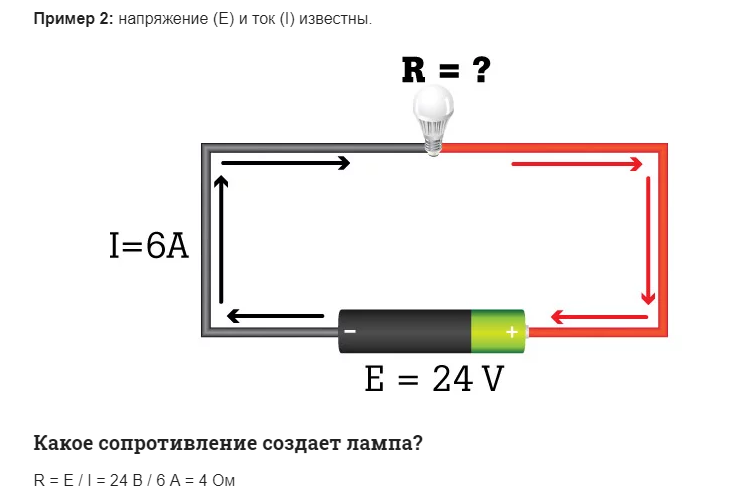
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Закон Ома в интегральной форме
Для работы с этой методикой можно воспользоваться дифференциальным выражением (J = p*E).
Пояснительные данные к интегральной форме расчета
Базовую формулу преобразуют следующим образом:
- в обе части добавляют множитель, учитывающий элементарный отрезок длины проводника (dL);
- взяв первый интеграл по контрольным точкам, получают итоговое значение для сопротивления: R = p*(L/S);
- совмещают две формулы (1 и 2), выполняют математическое преобразование;
- интеграл второй части определит значение напряжения.
Итоговый результат соответствует определению классического вывода Ома, где взаимная связь u r I обоснована результатом экспериментов (I = U/R).
Законы Кирхгофа
Законы Кирхгофа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Применение правил Кирхгофа к цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров. В этом случае законы формулируются следующим образом.
Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.
Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:
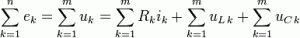
Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве , то она описывается уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
На этом рисунке для каждого проводника обозначен протекающий по нему ток (буквой «I») и напряжение между соединяемыми им узлами (буквой «U»)
Например, для приведённой на рисунке цепи, в соответствии с первым законом выполняются следующие соотношения:
Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например здесь, токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными. В соответствии со вторым законом, справедливы соотношения:
В соответствии со вторым законом, справедливы соотношения:
Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), перепад напряжения считается положительным, в противном случае — отрицательным.
Законы Кирхгофа, записанные для узлов и контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и напряжения.
Существует мнение, согласно которому «Законы Кирхгофа» следует именовать «Правилами Кирхгофа», ибо они не отражают фундаментальных сущностей природы (и не являются обобщением большого количества опытных данных), а могут быть выведены из других положений и предположений.
Закон Ома для неоднородного участка цепи
В реальных условиях для поддержания перемещения зарядов с определенной интенсивностью необходимо приложение сторонних сил, а не только кулоновских. Рассмотренный ниже пример демонстрирует участок замкнутой цепи, который называют неоднородным.
Описание закона
Формулировка этого принципа справедлива для любых двух точек цепи, по которой проходит электрический ток. Для этого примера формула Ома принимает следующий вид:
I = U12/R, где U12 обозначает напряжение между контрольными точками.
С учетом отмеченных на рисунке параметров можно преобразовать итоговое выражение следующим образом:
I = ((ϕ1- ϕ2) ± E)/R12,
где:
- ϕ1- ϕ2 – разница потенциалов;
- Eип – электродвижущая сила, которую характеризуют величина и определенная полярность;
- R12 – полное электрическое сопротивление (проводник + источник ЭДС).
Для пояснения полученного результата следует отметить наличие кулоновских и сторонних сил с векторами ЭДС Eq и Est, соответственно. При перемещении определенного заряда (q) между контрольными точками (1-2) по проводнику будет выполнена работа A12. Зависимости между этими величинами величины можно определить простой формулой:
A12/q = ϕ1 – ϕ2.
Так как ЭДС на участке будет равна работе по перемещению q, справедливо выражение:
Ast/q = E12.
Суммарное значение выполненных действий будет равно напряжению:
U = A12/q + Aип/q = ϕ1 – ϕ2 + E12.
После математического преобразования по закону Ома формула приобретает вид:
I = ((ϕ1- ϕ2) ± E)/R12.
Важно! Значение ЭДС может быть положительным либо отрицательным. Соответствующие изменения зависят от подключения источника в участок с определенной полярностью
Для корректного применения представленных правил можно рассмотреть пример расчета со следующими исходными данными:
- ЭДС – Eип = 5 V;
- потенциалы в отдельных точках – ϕ1 (ϕ2) = 20V (8V);
- электрическое сопротивление цепи – R12 = 4 Ом;
- сопротивление источника питания – Rип = 2 Ом.
Так как направление тока при замыкании цепи выбирается от большего потенциала к меньшему, по представленной на рис. выше схеме ЭДС берут со знаком «минус». Подставленные в рассмотренную формулу исходные данные помогут сделать следующее вычисление:
I = ((ϕ1- ϕ2) – Eип)/(R12 + Rип) = (20 – 8 – 5)/(4 + 2) = 7/6 ≈ 1,17 А.
К сведению. Обратный вариант включения ЭДС при аналогичных исходных параметрах сопровождается изменением знака на «минус».
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.

Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
где P – мощность, измеряется в ваттах и обозначается ВтU – напряжение, измеряется в вольтах и обозначается буквой ВI – сила ток, измеряется в амперах и обозначается буквой А.
Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
Бытовая сеть переменного тока
Пример №1. Проверка ТЭНа.
В стиральную машину встроен трубчатый электронагреватель 1,25 кВт на 220 вольт. Требуется проверить его исправность замером сопротивления.По мощности рассчитываем ток и сопротивление.
Проверяем расчет сопротивления калькулятором по току и напряжению. Данные совпали. Можно приступать к электрическим замерам.
Пример №2. Проверка сопротивления двигателя
Допустим, что мы купили моющий пылесос на 1,6 киловатта для уборки помещений. Нас интересует ток его потребления и сопротивление электрического двигателя в рабочем состоянии. Считаем ток:
Вводим в графы калькулятора напряжение 220 вольт и ток 7,3 ампера. Запускаем расчет. Автоматически получим данные:
- сопротивление двигателя — 30,1 Ома;
- мощность 1600 ватт.
Цепи постоянного тока
Рассчитаем сопротивление нити накала галогенной лампочки на 55 ватт, установленной в фаре автомобиля на 12 вольт.
Считаем ток:
Вводим в калькулятор 12 вольт и 4,6 ампера. Он вычисляет:
- сопротивление 2,6 ома.
- мощность 5 ватт.
Здесь обращаю внимание на то, что если замерить сопротивление в холодном состоянии мультиметром, то оно будет значительно ниже. Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников
Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложной пускорегулирующей аппаратуры, необходимой для светодиодных и люминесцентных светильников.
Другими словами: изменение сопротивления вольфрама при нагреве до раскаленного состояния ограничивает возрастание тока через него. Но в холодном состоянии металла происходит бросок тока. От него нить может перегореть.
Для продления ресурса работы подобных лампочек используют схему постепенной, плавной подачи напряжения от нуля до номинальной величины.
В качестве простых, но надежных устройств для автомобиля часто используется релейная схема ограничения тока, работающая ступенчато.
При включении выключателя SA сопротивление резистора R ограничивает бросок тока через холодную нить накала. Когда же она разогреется, то за счет изменения падения напряжения на лампе HL1 электромагнит с обмоткой реле KL1 поставит свой контакт на удержание.
Он зашунтирует резистор, чем выведет его из работы. Через нить накала станет протекать номинальный ток схемы.
Действие электродвижущих сил
Электродвижущая сила (ЭДС) является скалярной величиной, характеризующей работу не электрических сил, заставляющих производить разность потенциалов на выходе.
Дополнительная информация. Скалярная величина – это когда она может быть выражена только определённым значением. В отличие от векторной величины, которая определяется не только значением, но и направлением.
Используется ЭДС в генераторах, преобразующих какую либо работу А (джоуль) в электрическую. Для этого могут быть использованы такие виды энергии по их происхождению:
- Механическая индукционная. Вывод ЭДС возникает при пересечении проводником линий магнитного поля;
- Механическая пьезоэлектрическая. Возникновение ЭДС происходит при деформации некоторых веществ;
- Световая энергия. Здесь ЭДС появляется в полупроводниках при действии на них световых лучей;
- Термическая энергия. ЭДС образуется, когда контакты из разнородных проводников находятся под разными температурами;
- Химическая энергия. Возникновение ЭДС происходит вследствие химических реакций.
В зависимости от характера энергии и устройства генератора ЭДС может возникать как переменная, так и постоянная. Переменная может быть как синусоидальная (магнитные индукционные генераторы), так и импульсная (пьезозажигалки). Постоянную ЭДС преобразуют в основном из химической (элементы питания, аккумуляторы), световой (фотоэлементы) энергий и температуры (элементы Пельтье).

Генераторы тока
ЭДС образует на разноименных проводниках разность потенциалов. Если не соединять проводником клеммы, на которых имеется разность потенциалов, то тока в цепи не будет. Следовательно, никакой энергии не будет израсходовано. На клеммах будет оставаться разность потенциалов. Работу для поддержания этой разности совершать не надо.
Если к клеммам с разностью потенциалов подключить проводник с нагрузкой, то через него будет протекать электрический ток, выполняя работу в нагрузке. При этом разность потенциалов на клеммах будет стремиться к 0, что приведёт к падению тока до 0. Для поддержания разности потенциалов стабильной величиной необходимо, чтобы ЭДС получала энергию. Эта энергия затрачивает работу, равную той, которая совершается в нагрузке.
Отображение в дифференциальной форме
На подсчёт сопротивления влияет тип материи, по которой протекает электроток, а также геометрические габариты проводника.
Дифференциальная форма формулировки Ома, записывающаяся достаточно кратко, отображает электропроводящие характеристики изотропных материалов и заключается в умножении удельной проводимости на вектор напряжённости электрополя с целью вычисления вектора плотности энерготока.
Для выполнения требуемых вычислений, уравнение сформулируйте по закону ома:

Интересно!
Если исходить из научных данных, следует сделать вывод о законе ома в дифференциальной форме об отсутствии зависимого соотношения геометрических габаритов.
При использовании анизотропеновых электроэлементов нередко встречается несовпадение вектора плотности токового энергонапряжения. Данное суждение справедливо для закона ома в интегральной и дифференциальной формах.
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
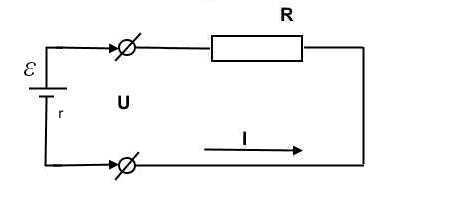
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:

Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:
Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
Интерпретация
Определяющаяся действием приложенного напряжения мощностная сила тока является пропорциональной показателю его напряжения. К примеру, при двойном увеличении приложенного напряжения, интенсивность постоянного тока также удваивается.
Интересно!
Наиболее часто правило Ома применяется для металла и керамики.
Методы запоминания формулы
Чтобы легче запомнить формулу расчёта напряжения на участке цепи, следует выписать на бумажном листе все величины, из которых она состоит, в которую также входит сопротивление и сила тока. Искомую величину закрыть пальцем, вследствие чего соотношение оставшихся величин будет отображать действие, которое необходимо совершить для её вычисления.
Ниже будет представлено видео с подробным объяснением всех правил и формул, относящихся к рассматриваемой теме.
Закон Ома – один из самых несложных для понимания, который входит в программу школьных учебников физики начального уровня. Пользуясь графическим приёмом расчёта величин – при необходимости или для самопроверки, можно получить безошибочные результаты вычислений.
Читайте также: Для чего нужные диэлектрические перчатки и как их проверяют?
Мнемоническая схема
Согласно мнемосхеме, чтобы высчитать электросопротивление по закону ома для участка цепи постоянного тока, необходимо комплексное напряжение на участке цепи разделить на силу тока для полной цепи. Однако, с физико-математической точки зрения, формулу ома для участка цепи для вычисления только по первому закону ома принято считать неполной.
Альтернативный способ вычислить токовое сопротивление по закону ома кратко подразумевает умножение электросопротивления материи, из которой выполнен проводник, на длину с последующим делением на площадь пересекающегося сечения.
Для выполнения вычислений сформулируйте по закону ома для участка цепи уравнение, исходя из имеющихся числовых данных:
Читайте также: Как выбрать микроомметр, или О значимости измерительного тока при измерении электрического сопротивления контактов выключателей
Применение закона Ома
Закон Ома используют, в частности, для градуировки шкал электроизмерительных приборов. Если к чувствительному гальванометру последовательно присоединить большое сопротивление, то такой прибор можно использовать для измерения напряжения, то есть в качестве вольтметра, который включают параллельно потребителя электроэнергии. Для обеспечения точности измерений через вольтметр должен проходить незначительный ток по сравнению с током потребителя ( I В < < I I_В << I IВ<
R Д = ( n − 1 ) R В R_Д = (n-1) R_В RД=(n−1)RВ
где R В R_В RВ – внутреннее сопротивление вольтметра.
Амперметром измеряют силу тока цепи, включая его последовательно с потребителем, поэтому во избежание искажений результатов измерений сопротивление амперметра должно быть значительно меньше сопротивления потребителей тока ( R А > > R R_А >> R RА>>R). Для расширения в n n n раз предела измерений параллельно вводу амперметра присоединяют шунт, то есть проводник, сопротивление которого значительно меньше внутреннего сопротивления амперметра: R Ш < < R А R_Ш << R_А RШ<
R Ш = R А / ( n − 1 ) R_Ш = R_А/(n-1) RШ=RА/(n−1)
Применение на линии электропередач
В процессе доставки на линию электропередач потери энергии должны быть минимизированы. Причиной энергетических потерь является нагрев провода, во время которого энергия электротока превращается в теплоэнергию.
Чтобы дать определение по закону ома потерянной мощности, необходимо показатель электрической мощности во второй степени умножить на внутреннее сопротивление источника напряжения и разделить на ЭДС в квадрате.
Из этого следует, что рост потери энергомощности осуществляется пропорционально протяжённости линии электропередач и квадрату электродвижущей силы.

Поскольку электродвижущую силу ограничивает прочность обмотки генератора, то повышение энергонапряжения возможно после того, как из генератора выйдет электроток, на участке входа линии.
Переменный ток легче всего распределяется по линии через трансформатор. Однако, поскольку следствием повышения энергонапряжения является потеря коронирования, а надёжность изоляции обеспечивается с трудом, напряжение на участке цепи протяжённой линии электропередач не превышает миллиона вольт.
Внимание!
Поведение линии электропередач в пространстве подобно антенне, ввиду чего берётся во внимание потеря на излучение.



