Сила Лоренца: формула, правило левой руки для определения направления силы, применение

 

Немного истории

Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.

В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.

И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».

Определение и формула

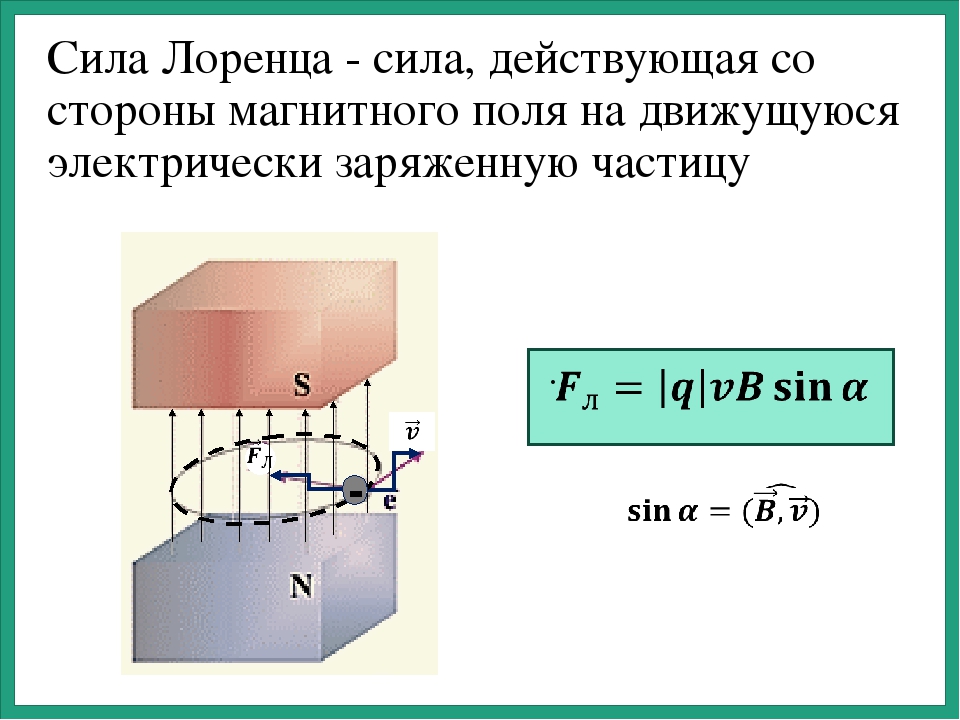
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.

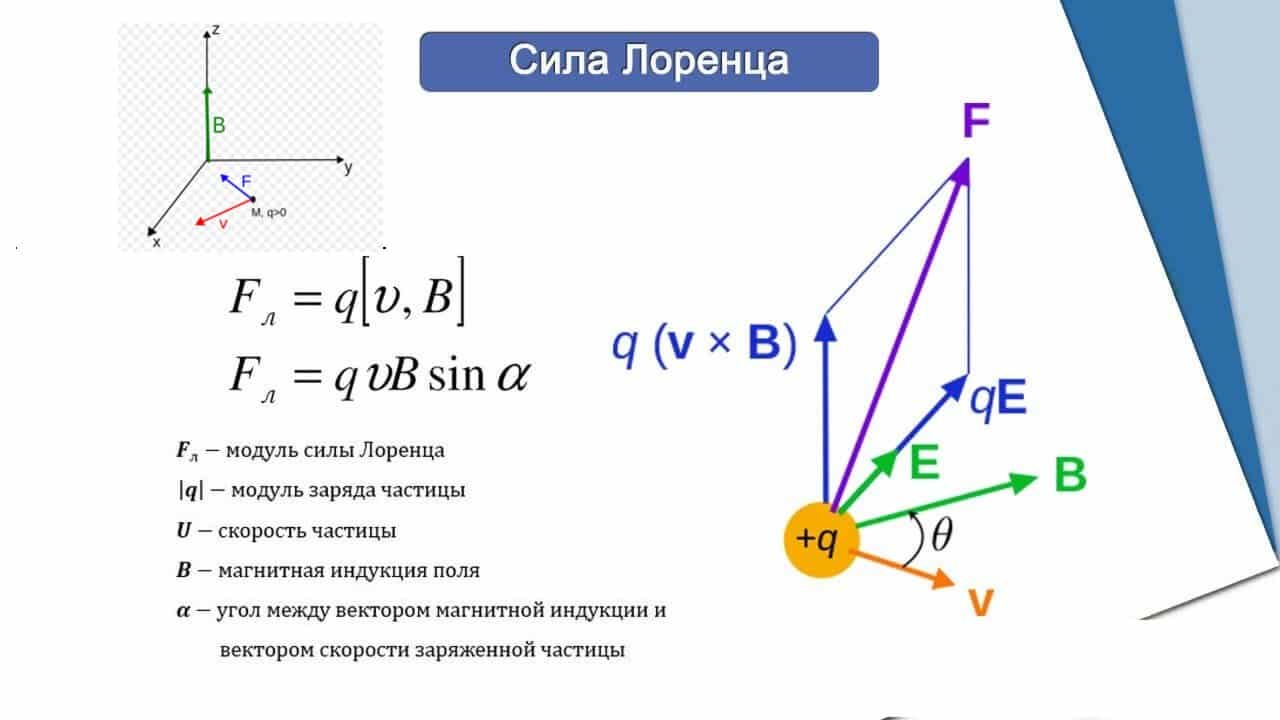
Рис. 1. Выводы Лоренца

Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.

По закону Ампера:

Учитывая, что

(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:

Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:

Модуль F вычисляется по формуле:

Из формулы следует:

1. Сила Лоренца приобретает максимальное значение, если угол α прямой.
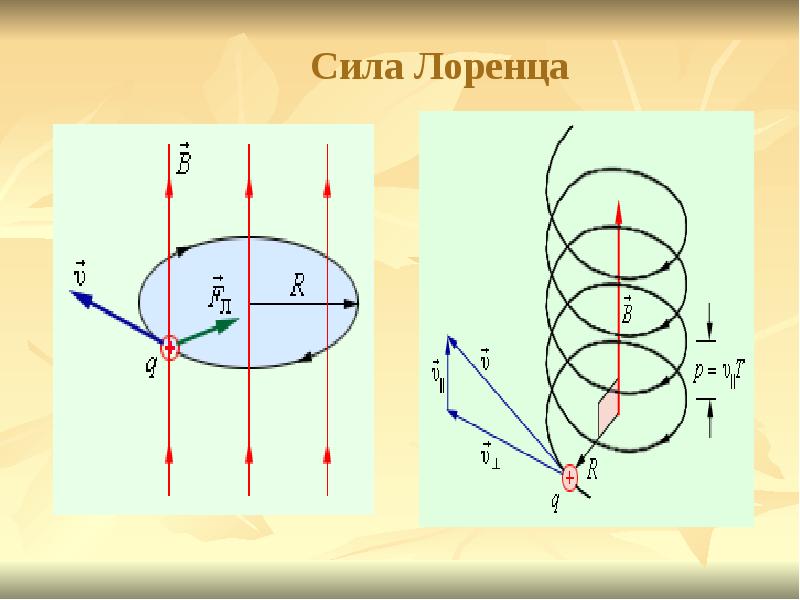
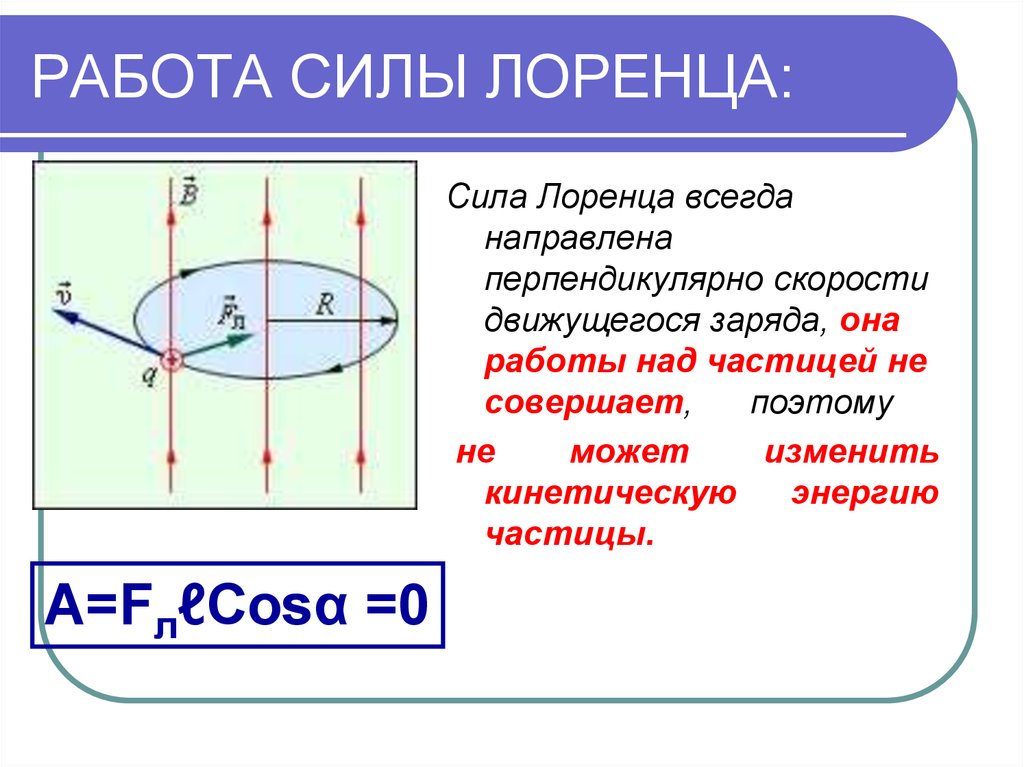
2. Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
3. Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).

Рис. 2. Заряженная частица между полюсами магнитов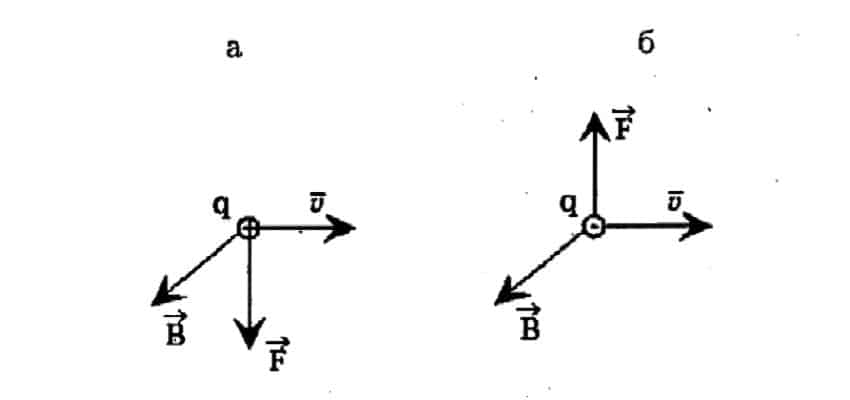
Рис. 3. Ориентация вектора в зависимости от полярности заряда

Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).

Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.

В чём измеряется?

Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0<к<1, а="" n="" –="" порядок="" числа="">

Когда возникает?

Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.

Для возникновения силы Лоренца необходимо выполнить три условия:

1. У частицы должен быть отрицательный или положительный заряд.
2. Заряженная частица должна находиться в магнитном поле.
3. Частица должна быть в движении, то есть вектор v ≠ 0.

Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.

Формула силы Лоренца при наличии магнитного и электрического полей

Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:

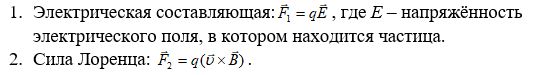
Тогда:

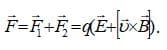
Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.

Направление силы Лоренца

Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.

Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).

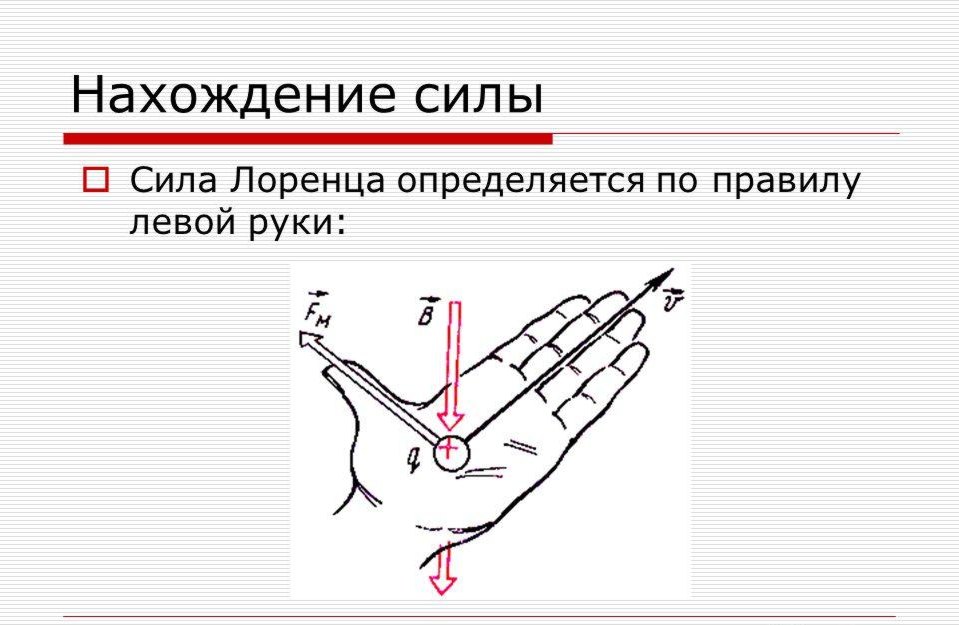
Рис. 4. Нахождение вектора силы Лоренца

Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.

Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.

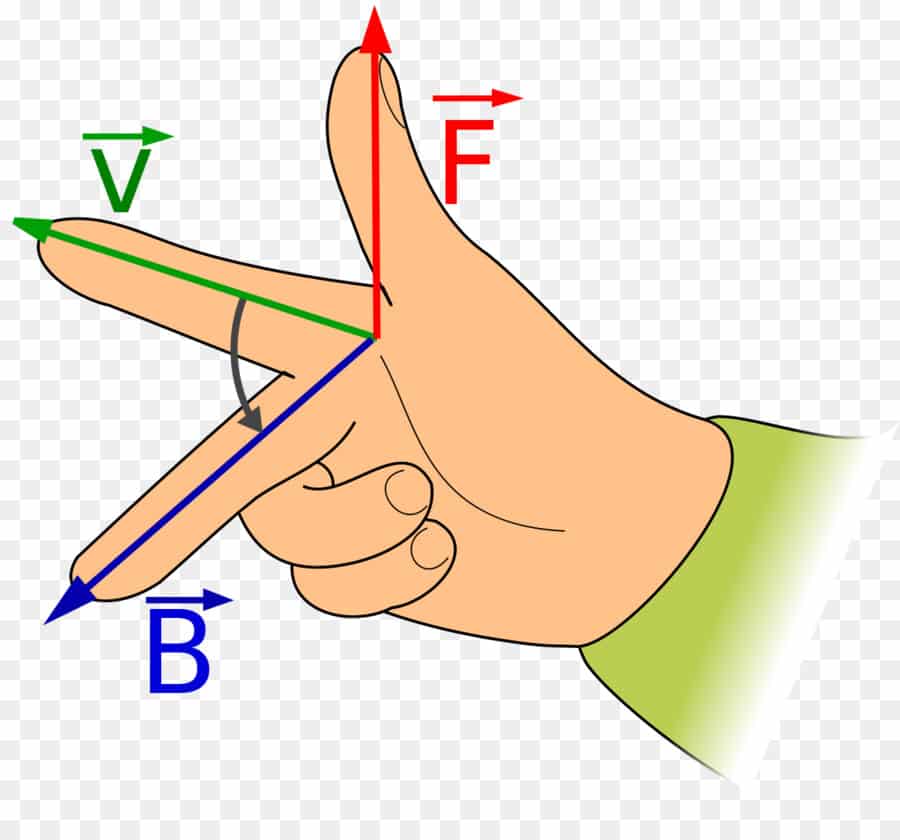
Рис. 5. Пример применения правила правой руки

Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.

Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.

Интересно!

Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица. Все остальные манипуляции остаются прежними.

Следствия свойств силы Лоренца

Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:

FЛ=qvBsinα,

sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.

Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.

В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:

R=mvqB

Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.

Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:

R=mvsinαqB

h=2mvcosαqB

Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.

Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.

Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.

Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.

Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.

Формула силы Лоренца при наличии магнитного и электрического полей

Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:

FЛ=qE+vB

где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.

Единицы измерения силы Лоренца

Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.

Понятие напряженности электрического поля

Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.

То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.

Напряженность электрического поля

Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:

E=Fq

Единицей измерения является Н/Кл или В/м.

Примеры задачи

Задача 1

На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.

Дано: q = 0,005 Кл B = 0,3 Тл v = 200 м/с α = 450

Решение: В условиях задачи нет упоминания электрического поля, поэтому силу Лоренца можно найти по следующей формуле: FЛ=qvBsinα=0,005×200×0,3×sin 450 =0,3×22=0,21 Н

Задача 2

Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.

Дано: q = 0,005 Кл B = 2 Тл FЛ = 32 Н α = 900

Решение: Чтобы найти скорость заряда, необходимо несколько видоизменить формулу для нахождения силы Лоренца:   FЛ=qvBsinαv=FЛqBsinα v=320,005×2×sin900=320,01×1=32000мс=32 км/с

Задача 3

Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н. Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.

Дано: q = -1,6 × 10-19 Кл B = 0,05 Тл FЛ = 5 × 10-13 Н α = 900

Решение: В этой задаче сила Лоренца ко всему прочему еще и заставляет двигаться электрон по окружности. Поэтому здесь под ускорением следует понимать центростремительное ускорение: aц=v2R На данный момент неизвестны ни скорость электрона, ни радиус окружности, по которой он движется.   v=FЛqBsinα=5×10-13-1,6×10-19×0,05∙sin900=6×107мс R=mvqB=9×10-31×6×107-1,6×10-19×0,05=6,8×10-3мс

aц=v2R=6×10726,8×10-3=5×1017мс2

Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.

 

Что такое сила Лоренца — определение, когда возникает, получение формулы

Известно, что электрический ток – это упорядоченное перемещение заряженных частиц. Установлено также, что во время движения в магнитном поле каждая из этих частиц подвергается действию силы. Для возникновении силы требуется, чтобы частица находилась в движении.

Сила Лоренца – это сила, которая действует на электрически заряженную частицу при её движении в магнитном поле. Её направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Равнодействующая сил Лоренца и есть сила Ампера. Зная ее, можно вывести формулу для силы Лоренца.

Время, требуемое для прохождения частицей отрезка проводника,
, где
, где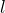
– длина отрезка,
– скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника,
– скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника,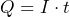
. Подставив сюда значение времени из предыдущего равенства, имеем

                             (2)

В то же время
, где
, где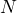
– количество частиц, находящееся в рассматриваемом проводнике. При этом
, где
, где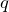
– заряд одной частицы. Подставив в формулу значение
из (2), можно получить:

Таким образом,

Используя (1), предыдущее выражение можно записать как

После сокращений и переносов появляется формула для вычисления силы Лоренца

С учетом того, что формула записана для модуля силы, ее необходимо записать так:

                            (3)

Поскольку
, то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что
, то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что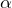
– это угол, образуемый векторами скорости частицы и магнитной индукции.

Запись формулы в векторном виде будет выглядеть следующим образом:

– это векторное произведение, результатом которого является вектор с модулем, равным
– это векторное произведение, результатом которого является вектор с модулем, равным
.

Исходя из формулы (3), можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности направлений электрического тока и магнитного поля, то есть при
, и исчезать при их параллельности (
, и исчезать при их параллельности (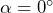
).

Необходимо помнить, что для получения правильного количественного ответа – например, при решении задач, – следует пользоваться единицами системы СИ, в которой магнитная индукция измеряется в теслах (1 Тл = 1 кг·с−2·А−1), сила – в ньютонах (1 Н = 1 кг·м/с2), сила тока – в амперах, заряд в кулонах (1 Кл = 1 А·с), длина – в метрах, скорость – в м/с.

Определение направления силы Лоренца с помощью правила левой руки

Поскольку в мире макрообъектов сила Лоренца проявляется как сила Ампера, для определения ее направления можно пользоваться правилом левой руки.

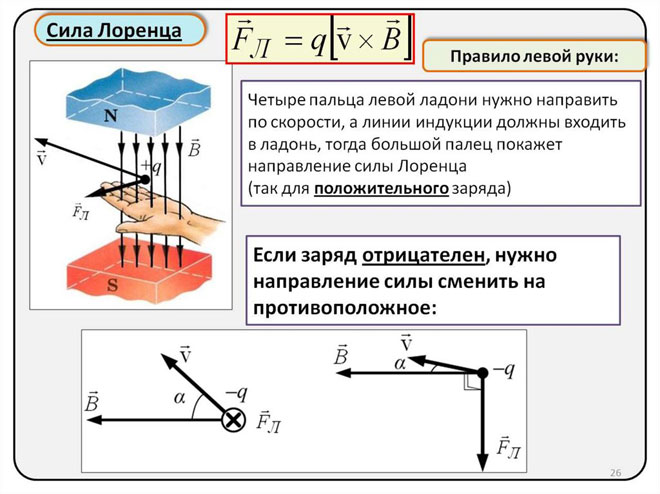
Нужно поставить левую руку так, чтобы раскрытая ладонь находилась перпендикулярно и навстречу линиям магнитного поля, четыре пальца следует вытянуть в направлении силы тока, тогда сила Лоренца будет направлена туда, куда указывает большой палец, который должен быть отогнут.

Движение заряженной частицы в магнитном поле

В простейшем случае, то есть при ортогональности векторов магнитной индукции и скорости частицы сила Лоренца, будучи перпендикулярной к вектору скорости, может менять только её направление. Величина скорости, следовательно, и энергия будут оставаться неизменными. Значит, сила Лоренца действует по аналогии с центростремительной силой в механике, и частица перемещается по окружности.

В соответствии со II законом Ньютона (
) можно определить радиус вращения частицы:

.

Необходимо обратить внимание, что с изменением удельного заряда частицы (
) меняется и радиус.

При этом период вращения T =
=
=
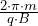
. Он не зависит от скорости, значит, взаимное положение частиц с различными скоростями будет неизменным.

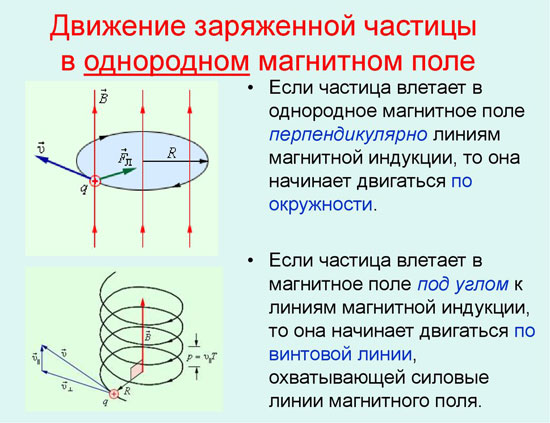
В более сложном случае, когда угол между скоростью частицы и напряженностью магнитного поля является произвольным, она будет перемещаться по винтовой траектории – поступательно за счет составляющей скорости, направленной параллельно полю, и по окружности под влиянием ее перпендикулярной составляющей.

Применение силы Лоренца в технике

Кинескоп

Кинескоп, стоявший до недавнего времени, когда на смену ему пришел LCD-экран (плоский), в каждом телевизоре, не смог бы работать, не будь силы Лоренца. Для формирования на экране телевизионного растра из узкого потока электронов служат отклоняющие катушки, в которых создается линейно изменяющееся магнитное поле. Строчные катушки перемещают электронный луч слева направо и возвращают обратно, кадровые отвечают за вертикальное перемещение, двигая бегающий по горизонтали луч сверху вниз. Такой же принцип используется в осциллографах – приборах, служащих для изучения переменного электрического напряжения.

Масс-спектрограф

Масс-спектрограф – прибор, использующий зависимость радиуса вращения заряженной частицы от ее удельного заряда. Принцип его работы следующий:

Источник заряженных частиц, которые набирают скорость с помощью созданного искусственно электрического поля, с целью исключения влияния молекул воздуха помещается в вакуумную камеру. Частицы вылетают из источника и, пройдя по дуге окружности, ударяются в фотопластинку, оставляя на ней следы. В зависимости от удельного заряда меняется радиус траектории и, значит, точка удара. Этот радиус легко измерить, а зная его, можно вычислить массу частицы. С помощью масс-спектрографа, например, изучался состав лунного грунта.

Циклотрон

Независимость периода, а значит, и частоты вращения заряженной частицы от её скорости в присутствии магнитного поля используется в приборе, называемом циклотроном и предназначенном для разгона частиц до высоких скоростей. Циклотрон – это два полых металлических полуцилиндров – дуанта (по форме каждый из них напоминает латинскую букву D), помещенных прямыми сторонами навстречу друг другу на небольшом расстоянии.

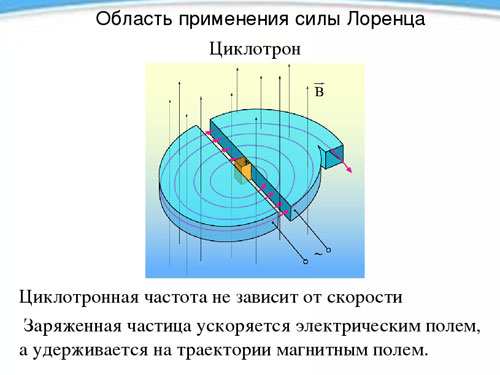
Дуанты помещаются в постоянное однородное магнитное поле, а между ними создается переменное электрическое поле, частота которого равна частоте вращения частицы, определяемой напряженностью магнитного поля и удельным зарядом. Попадая дважды за период вращения (при переходе из одного дуанта в другой) под воздействие электрического поля, частица каждый раз ускоряется, увеличивая при этом радиус траектории, и в определенный момент, набрав нужную скорость, вылетает из прибора через отверстие. Таким способом можно разогнать протон до энергии в 20 МэВ (мегаэлектронвольт).

Магнетрон

Устройство, называемое магнетроном, который установлен в каждой микроволновой печи, – еще один представитель приборов, использующих силу Лоренца. Магнетрон служит для создания мощного СВЧ-поля, которое разогревает внутренний объем печи, куда помещается пища. Магниты, входящие в его состав, корректируют траекторию движения электронов внутри прибора.

Магнитное поле Земли

А в природе сила Лоренца играет крайне важную для человечества роль. Её наличие позволяет магнитному полю Земли защитить людей от смертоносного ионизирующего излучения космоса. Поле не дает возможности заряженным частицам бомбардировать поверхность планеты, заставляя их менять направление движения.

Траектории частиц под действием силы Лоренца

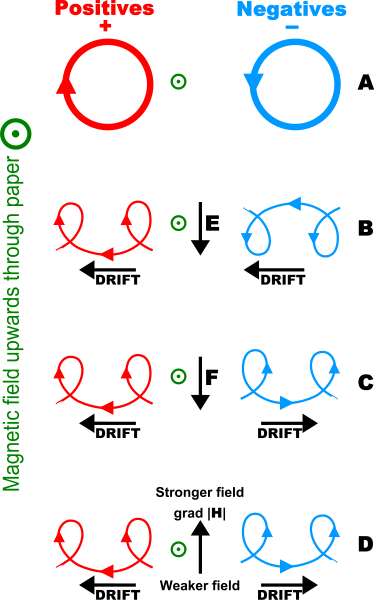
Заряженная частица дрейфует в однородном магнитном поле. (A) Нет возмущающей силы (B) В электрическом поле, E (C) С независимой силой, F (например, гравитация) (D) В неоднородном магнитном поле, grad H

Во многих случаях, представляющих практический интерес, движение в магнитном поле электрически заряженной частицы (например, электрона или иона в плазме) можно рассматривать как суперпозицию относительно быстрого кругового движения вокруг точки, которая дрейфует в направлении перпендикулярном электрическому и магнитным полям. Скорости дрейфа могут различаться в зависимости от их зарядового состояния, массы или температуры, что может привести к электрическим токам или химическому разделению.

Значение силы Лоренца

В то время как современные уравнения Максвелла описывают то, как электрически заряженные частицы и токи или движущиеся заряженные частицы вызывают электрические и магнитные поля, сила Лоренца дополняет эту картину, описывая силу, действующую на движущийся точечный заряд q в присутствии электромагнитных полей. Хотя сила Лоренца описывает действие E и B на точечный заряд, но такие электромагнитные силы не являются всей картиной. Заряженные частицы, возможно, связаны с другими силами, особенно с гравитацией и ядерными силами. Таким образом, уравнения Максвелла не отделены от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца — это один из аспектов; генерация E и B токами и зарядами — другое.

В реальных материалах сила Лоренца неадекватно описывает коллективное поведение заряженных частиц как в принципе, так и с точки зрения вычислений. Заряженные частицы в материальной среде не только реагируют на поля E и B, но и создают эти поля сами. Для определения временной и пространственной реакции зарядов необходимо решать сложные уравнения переноса, например, уравнение Больцмана, уравнение Фоккера — Планка или уравнения Навье — Стокса . Например, см. Магнитогидродинамику, гидродинамику, электрогидродинамику, сверхпроводимость, звездную эволюцию . Разработан целый физический аппарат для решения этих вопросов. См., Например, формулы Грина — Кубо и функцию Грина (теория многих тел) .

ЭДС

Магнитная сила (qv × B) в выражении силы Лоренца отвечает за двигательную электродвижущую силу (или двигательную ЭДС), явление, лежащее в основе действия многих электрических генераторов. Когда проводник перемещается через область магнитного поля, магнитное поле оказывает противоположно направленные силы на электроны и ядра в проводе, и это создает ЭДС. Термин «двигательная ЭДС» применяется к этому явлению, поскольку ЭДС возникает из-за движения провода.

В других электрических генераторах магниты движутся, а проводники — нет. В этом случае ЭДС возникает из-за электрической силы (qE) в уравнении для силы Лоренца. Рассматриваемое электрическое поле создается изменяющимся магнитным полем, приводящим к возникновению индуцированной ЭДС, как описано уравнением Максвелла — Фарадея.

Обе эти ЭДС, несмотря на их явно различное происхождение, описываются одним и тем же уравнением, а именно ЭДС — это скорость изменения магнитного потока через провод. Это закон электромагнитной индукции Фарадея, см. Ниже . Специальная теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами. Фактически, электрическое и магнитное поля представляют собой разные грани единого электромагнитного поля, и при переходе от одной инерциальной системы отсчета к другой часть электромагнитного векторного поля E можно полностью или частично заменить на B или наоборот.

Единицы измерения силы Лоренца

Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.

Понятие напряженности электрического поля

Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.

То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.

Напряженность электрического поля

Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:

Единицей измерения является Н/Кл или В/м.